Cryptography

In the last part we discussed about logging. In this part we are giving a rudimentary introduction to relevant cryptography concepts.

Introduction to HTTPS

The purpose of the HTTPS protocol is to enable secure web browsing. From the user point of view, it is important to know whether she connects to a website over an unsecure HTTP connection or over a secure HTTPS connection. Different browsers indicate this in different ways.

Next we see how an example of how a particular browser provides the indication. You should try to figure out how the indication works in all different browsers that you use.

The indicator of https protocol is a small lock next to the url:

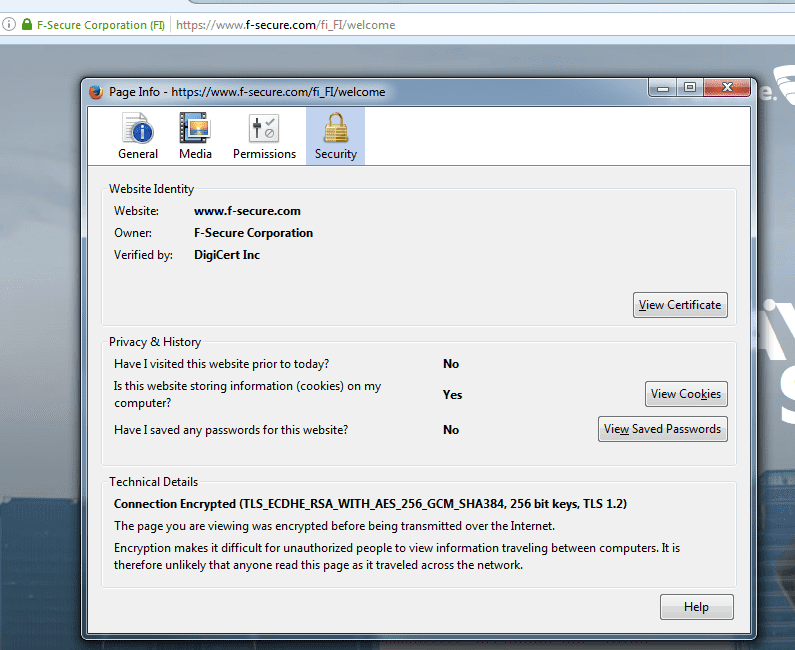
Let’s click the lock, then the right arrow and go for more information. We get something that looks like this:

This tab provides lots of information. We will take a closer look at many strange acronyms that appear under ”Technical details”.

What do these letters mean and why are they needed?

Basic concepts

First thing that may come to your mind when you hear the word ”cryptography” is about transforming normal messages into secret messages and back.

This is not a false impression but there is quite much more in cryptography as well.

But let us start with the basic setting and define some basic terms.

We call the original message that is supposed to be kept hidden the plaintext. The idea of ciphering is to use some encryption function and some encryption key to get the cryptotext. That is the message in the hidden form. For the reverse direction, we need a decrypting function, a method that is used together with a decryption key in order to retrieve the original plaintext.

Encryption is used to protect confidentiality of the data.

An important building block in cryptography is a one-way function (OWF). An OWF is a function that, from the one hand, can be efficiently evaluated. This means it is easy to calculate y = f(x) when x is given as an input. In this context ”easy” means something that is easily doable with the help of any kind of computer. On the other hand, it should be hard to invert the OWF. This means it is very difficult to find out x, if you only know f and y.

Cryptographic hash function is a special type of an OWF such that

• the output y is always of fixed length
• it is hard to find collisions.

A collision is a situation where two different inputs x and x’ give the same output: f(x) = f(x’).

SHA-256 and SHA-3 are two commonly used cryptographic hash functions. It you calculate the SHA-256 value of any binary string, the result is a random-looking string of 256 bits.

Because the length of the input is not restricted, it is obvious that many different inputs must exist that have the same output. But what is important is that no such collisions are known for the SHA-256 function.

The output of different variants of SHA-3 are of different length. However, there are no variants with a very short output length.

Q: Why a cryptographic hash function cannot have an output length of 3 bits?

All details of hash functions are publicly known and, in principle, anybody can calculate the hash value of any input. Sometimes it is useful that only a person who knows a secret key is able to calculate the hash value. Functions like this are called message authentication codes (MAC) and the value of the function is called the MAC value.

Let us assume that you know some secret key and you have received a message and a MAC value. If you now use the received message and the secret key as inputs to the functions and find out that the output of the function is equal to the received MAC value, then you can be reasonably sure that somebody who knows the secret key must have calculated the MAC value. In addition, you are able to conclude that the message has not been changed after the calculation of the MAC value on the sending side.

Summary: Message authentication codes are used to protect integrity of the data.

One of the commonly used methods for constructing a MAC function is hmac. It is built on top of some hash function, e.g. SHA-256 or SHA-3.

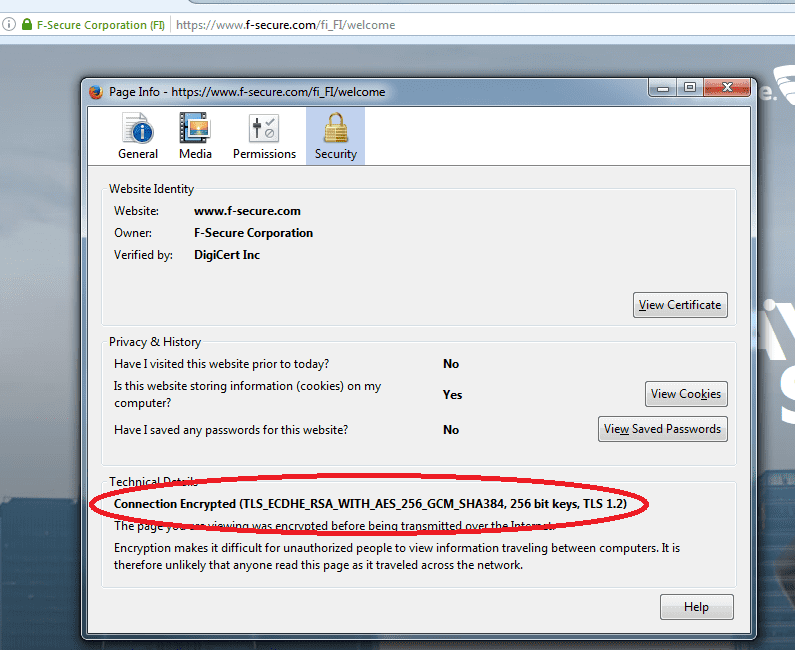
Our HTTPS example (TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384_256 bit keys,TLS 1.2) makes use of a SHA384 hash function.

Symmetric cryptography

All classical (i.e. more than 40 years old) ciphering methods are symmetric. This means that anybody who knows the function and the secret key needed for encrypting messages is also able to decrypt messages. In other words, encryption and decryption are in symmetric roles. The encryption function and the decryption function have very similar structures; sometimes they could even be equal to each other. The key used for encryption is the same key that is used for decryption; or at least each key can be derived from the other by some simple transformation.

There are nowadays also encryption methods that are not symmetric, i.e., being able to encrypt does not guarantee that you are able to decrypt even your own message. This kind of asymmetry is useful in many situations and we will discuss those later.

Symmetric encryption methods are still useful in many situations, and they are typically much faster than asymmetric ones. Therefore, symmetric encryption is in wide use, and new symmetric methods are developed. One-time pad (OTP) and AES are examples of symmetric encrypting schemes.

One of the oldest encryption methods is substituting every instance of a letter with some other letter. A cipher like this is called a substitution cipher. An example is the CAESAR cipher which is an encryption algorithm where you get the cryptotext by rotating every letter in the plaintext three positions forward in the alphabet. Decryption is done by rotating every letter of the cryptotext three positions backwards.

One-time pad (OTP) is one of the simplest encryption methods. To encrypt a message of, say, 140 bits you need a secret key of 140 bits. You compute the XOR of each message bit with the corresponding key bit, and you get 140 cryptotext bits,

The decrypting process is exactly the same as the encryption process. If you know the secret key you can decrypt the message by XORing bit-by-bit the cryptotext message and the key,

This works because

Although OTP is very simple and fast, it possesses some very good security properties. We are going to discuss those later.

The only downside of the OTP is that the key must be as long as the actual plaintext message. And you should not use the key more than once, hence the name ”one-time pad”.

Advanced Encryption Standard (AES) is a family of modern block ciphers. AES-256 has key size of 256 bits and it turns 128-bit plaintext blocks into 128-bit cryptotext blocks, and vice versa. This algorithm is quite fast even when implemented in software and considered secure enough for almost all uses. Many modern processors provide hardware support for AES.

Remember to check your points from the ball on the bottom-right corner of the material!